1. Berikut data banyaknya user dari pemakai internet di warnet :
| 148 | 175 | 148 | 120 |
| 160 | 176 | 155 | 130 |
| 155 | 170 | 165 | 140 |
| 173 | 157 | 178 | 150 |
Dari data tersebut :
a) Buat distribusi frekwensi dan histogramnya
b) Tanpa mengacu distribusi frekwensi,hitung nilai rata-rata, modus, median, rentang, rentang antara kuartil, simpangan kuartil, rata-rata simpangan ( rata-rata deviasi), simpangan baku (standar deviasi), variasi, koefisien variasi, kemiringan, dan kurtosis.
Jawab :
a) Range = 178 – 120 = 58
Banyak kelas= 1 + 3,3 log n = 1 + 3,3(log 16) = 1+3,3(1,2) = 1+3,96 = 4,96 = 5
p = 58/(4,96) = 11,7 = 12
Ujung bawah kecil interval pertama adalah 120 atau 119,5
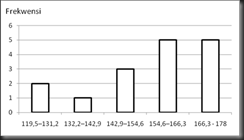
Daftar distribusi frekwensi :
| Kelas | Interval | Tabulasi | Frekwensi |
| 1 | 119,5 – 131,2 | II | 2 |
| 2 | 132,2 – 142,9 | I | 1 |
| 3 | 142,9 – 154,6 | III | 3 |
| 4 | 154,6 – 166,3 | IIIII | 5 |
| 5 | 166,3 – 178 | IIIII | 5 |
Histogram:
b) Rata-rata =
= 156,25
Modus =b + p*
= 145,5 + 12* 
Data terurut :
120,130,140,148,148,150,155,155,157,160,165,170,173,175,176,178
Median = b + p*
= 145,5 + 12 *
Rentang = data terbesar – data terkecil= 178 -120= 58
K1= data ke 
K2= data ke 
Rentang antar kuartil = K3-K1= 170 – 148= 22
Simpangan kuartil =
= 1/2 (170 – 148) = 11
Rata-rata simpangan (rata-rata deviasi)
Simpangan baku (standar deviasi)
Variansi = simpanganbaku2 =10,8332 = 117354
Koefisien variasi =
= 
Kemiringan
Kurtosis
2. Misalkan ruang sampel menyatakan populasi media penyimpanan data(disket dan CD) pada suatu kantor tertentu. Media penyimpanan data tersebut dikelompokkan menurut kondisinya :
| Barang | Baik | Rusak | Jumlah |
| CD | 460 | 40 | 500 |
| Disket | 140 | 260 | 400 |
| Jumlah | 600 | 300 | 900 |
Diadakan audit untuk mengetahui kondisi media penyimpanan data dikantor tsb. Dengan cara mengambil sampel secara acak pada kotak media penyimpanan. Bila media yang terpilih ternyata mempunyai kondisi baik, berapakah peluang yang terpilih itu media CD?
Jawab :
Diketahui :
M = media CD
E = dengan kondisi baik
30
3. Suatu generator telekomunikasi nirkabel mempunyai 3 pilihan tempat untuk membangun pemancar sinyalyaitu di daerah tengah kota, daerah kaki bukit di kota itu dan daerah tepi pantai, dengan masing-masing mempunyai peluang 0.2 ; 0.3 dan 0.5. Bila pemancar dibangun di tengah kota, peluang terjadi gangguan sinyal adalah 0.05. Bila pemancar dibangun di kaki bukit, peluang terjadinya gangguan sinyal adalah 0.06. Bila pemancar dibangun di tepi pantai, peluang terjadinya gangguan sinyal adalah 0.08.
a) Berapakah peluang terjadinya gangguan sinyal?
b) Bila diketahui telah terjadinya gangguan padas inyal, berapa peluang bahwa operator tersebut telah membangun pemancar di tepi pantai?
Jawab :
a) Peluang terjadinya gangguan sinyal
Diketahui :
A :tempat untuk membangun pemancar
B1 :peluang pemancar dibangun di tengah kota
B2 :peluang pemancar dibangun di kaki bukit
B3 :peluang pemancar dibangun di tepi pantai
Berdasarkan aturan penghapusan dapat ditulis :
= (0,2)(0,05) + (0,3)(0,06) + (0,5)(0,08)
= 0,01 + 0,018 + 0,04
= 0,068
b) Peluang telah terbangun pemancar di tepi pantai
4. Suatu pabrik computer melaporkan bahwa dari 100 pengiriman computer ke suatu took A terdapat 5 yang cacat. Bila suatu instansi membeli 10 komputer tersebut secara acak dari toko A, maka :
a) Berapakah probabilitas mengandung paling banyak satu komputer yang cacat.
b) Berapakah probabilitas minimum paling banyak 3 komputer yang cacat
c) Berapakah probabilitas maksimum paling banyak 4 komputer yang cacat
Jawab :
a) Probabilitas mengandung paling banyak satu komputer yang cacat.
Diketahui D=5, x≤1, N =100 dan n=10
p(x≤1) = p(x=0)+p(x=1)
b) Probabilitas minimum paling banyak 3 komputer yang cacat
Diketahui :
D = 5, x≤3, N=100, n=10
p(x ≤ 3) = p(x=0) + p(x=1) + p(x=2) + p(x=3)
c. Probabilitas maksimum paling banyak 4 komputer yang cacat
Diketahui :
D = 5, x≤4, N=100, n=10
p(x ≤ 4) = p(x=0) + p(x=4)
contoh aplikasi Distribusi Kontinyu dalam bidang Teknolog iInformasi.
Distribusi kontinyu merupakan salah satu macamdistribusiprobabilitas, yaitu model matematik yang menghubungkan nilai variabel dengan probabilitas terjadinya nilai itu. Dengan perkataan lain, kitadapat membayangkan diameter cincin piston sebagaivariabel random, karena diameter itu menjalani nilai-nilai yang berbeda dalam populasi itu menurut mekanisme random. Maka distribusi probabilitas diameter cincin menggambarkan probabilitas terjadinya setiap nilai diameter cincin di dalam populasi itu. Dimana untuk distribusi kontinyu variabel yang diukur dinyatakan dalam skala kontinyu.Oleh karena itu distribus iprobabilitasnya dinamakan distribusikontinyu.
Bentuk distribusi kontinyu adalah kurva yang halus, dengan luasan di bawah kurva sama dengan probabilitas, sehingga probabilitas bahwa x terletak di dalam interval dari a sampai b ditulis :
Contoh aplikasi dengan Distribusi kontinyu adalah, aplikasi forecaster, aplikasi pendeteksi bencana dan aplikasi survey
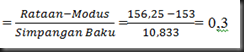
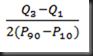
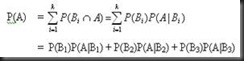
0 komentar:
Posting Komentar